Résolution d’équations, d’inéquations et de systèmes.¶
Equations et inéquations¶
Pour résoudre une équation (ou une inéquation) avec SimulaMath :
Saisir l’équation (ou l’inéquation) dans le panneau de gauche,
Spécifier la ou les variables dans la zone des variables,
Puis appuyez sur le bouton d’affichage.
La solution de l’équation \((x+1)(2x-5)(x^2+1)=0\) sur \(\mathbb{R}\).
Note
Vous devez spécifier les variables dans la zone des variables
Note
Vous pouvez également résoudre des équations dans un ensemble donné.
Résolution de l’équation \((x+1)(2x-5)(x^2+1)=0\) sur \(\mathbb{C}\)
Résolution avec des paramètres
Note
Si l’équation contient des variables qui ne sont pas définies dans la zone des variables, elles sont considérées comme des paramètres.
Résolvons l’équation \(ax+b = 0\) où \(x\in \mathbb{R}\).
La solution de l’inéquation \(x^2-3x+2 \geq 0\) dans \(\mathbb{R}\)
La résolution dans \(\mathbb{R}\) de \((x-1)(x+4)=0\text{ et } x>0\).
Systèmes linéaires et non linéaires¶
Pour entrer un système (ou une inéquation),
Saisissez d’abord la première équation (ou inéquation), puis appuyez sur la touche ENTREE ;
Saisissez ensuite la deuxième équation (ou inéquation) et appuyez sur ENTREE ;
Et ainsi de suite jusqu’à la dernière équation (ou inéquation).
La solution dans \(\mathbb{R}^2\) du système :
La résolution sur \(\mathbb{R}^3\) du système :
La résolution sur \(\mathbb{R}^3\) du système :
Équations différentielles¶
La résolution de l’équation différentielle \(y'''-3y''+3y'-y=0\)
La résolution de l’équation différentielle \(y'''-3y''+3y'-y=0\) avec les conditions initiales \(y(0) = 0 ; y'(0)=1\) et \(y''(0)=1\).
La résolution de l’équation différentielle \(y''+2y'+y=0\).
La solution de l’équation différentielle \(y''+2y'+y=0\) avec les conditions initiales \(y(0)=1\) et \(y'(0)=2\).
La solution de l’équation différentielle \(y''+y=\cos(x)\)
La solution de l’équation différentielle \(xy'-3y=(x+1)(x-3)\)
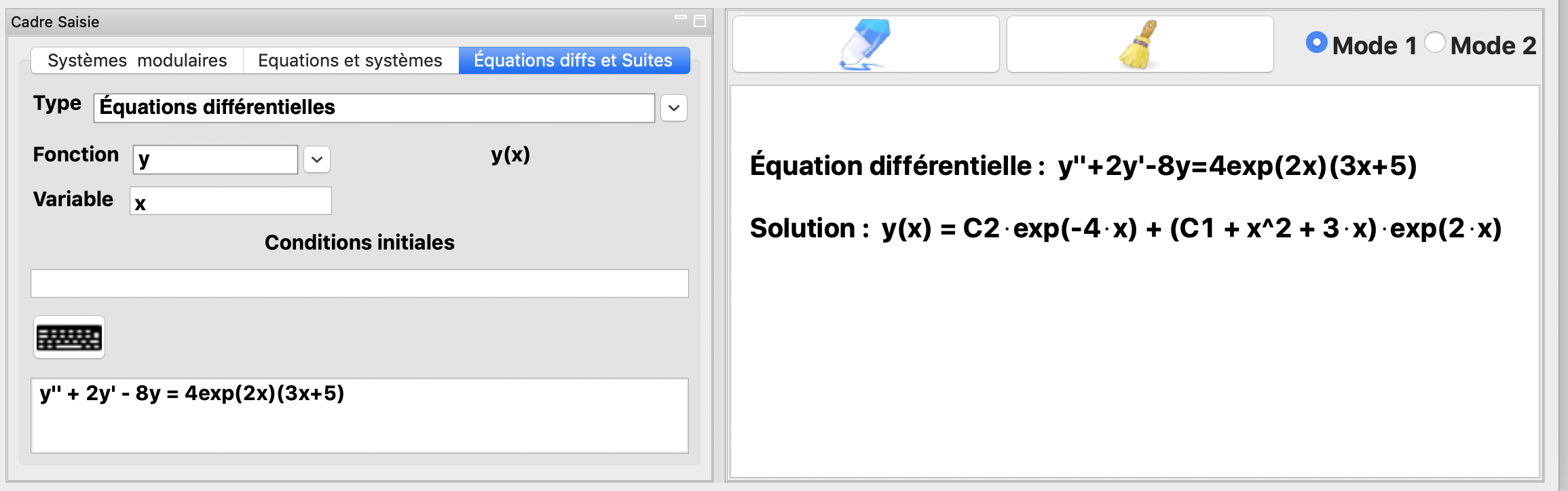
Résolution de l’équation différentielle \(y''+2y'-8y=4exp(2x)(3x+5)\)
Systèmes différentiels¶
La résolution du système différentiel
avec \(a\in \mathbb{R}\).
La résolution du système différentiel
La résolution du système différentiel
La résolution du système différentiel :
avec les conditions initiales \(f(0)=0 ; g(0)=1\) et \(h(0)=-1\).
Suites récurrentes linéaires¶
La solution de l’équation récurrente \(U(n+1)=U(n)+r\) avec \(r\in \mathbb{R}\).
La solution de l’équation récurrente \(U(n+1)=2U(n)+b\) avec \(b\in \mathbb{R}\) avec \(U(0)=1\).
La solution de l’équation récurrente \(U(n+2) -2U(n+1)+U(n)=0\).
Systèmes modulaires¶
La résolution de certains systèmes modulaires peut être effectuée en utilisant le théorème du reste chinois.
Exemple : résoudre le système modulaire