Résolution d’équations, d’inéquations et systèmes.¶
Équations et inéquations¶
Pour résoudre une équation (ou une inéquation) avec SimulaMath:
il faut saisir l’équation (ou l’inéquation) dans le panneau de gauche,
préciser la ou les variable(s) dans la zone des variables,
ensuite appuyer sur le bouton d’affichage.
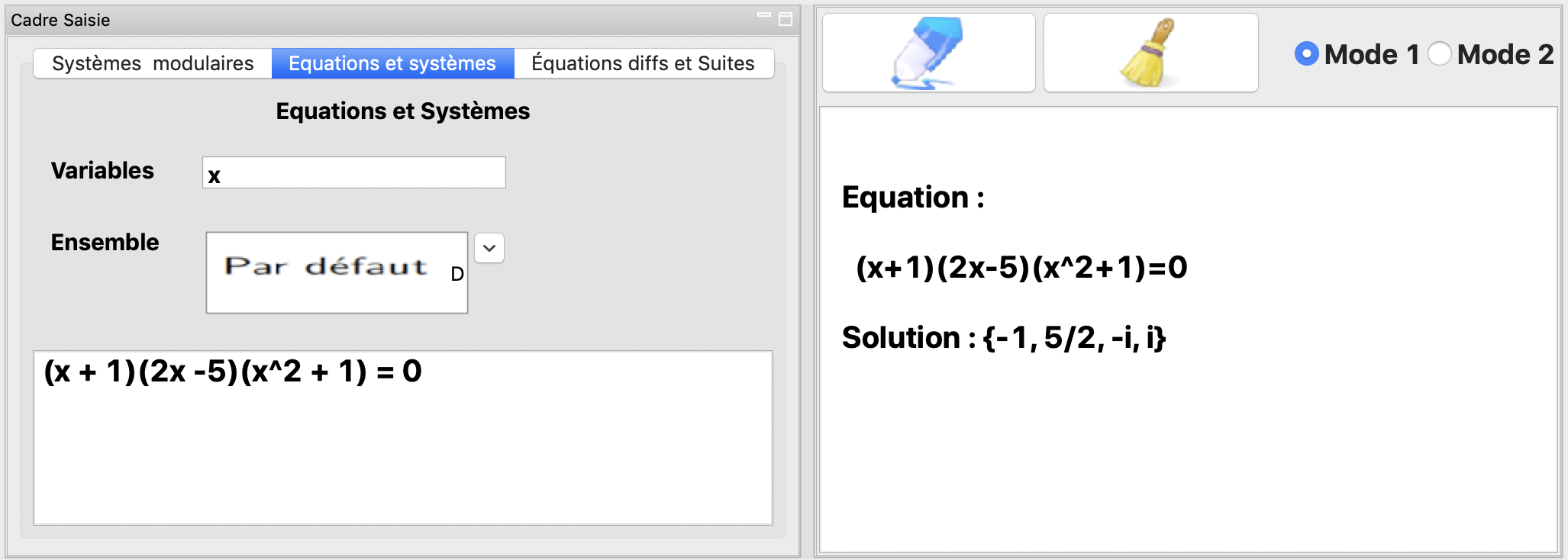
La résolution de l’équation \((x+1)(2x-5)(x^2+1)=0\). Si aucun ensemble n’est précisé, la résolution sera faite dans \(\mathbb{C}\).
Note
Vous devez préciser les variables dans la zone des variables
Note
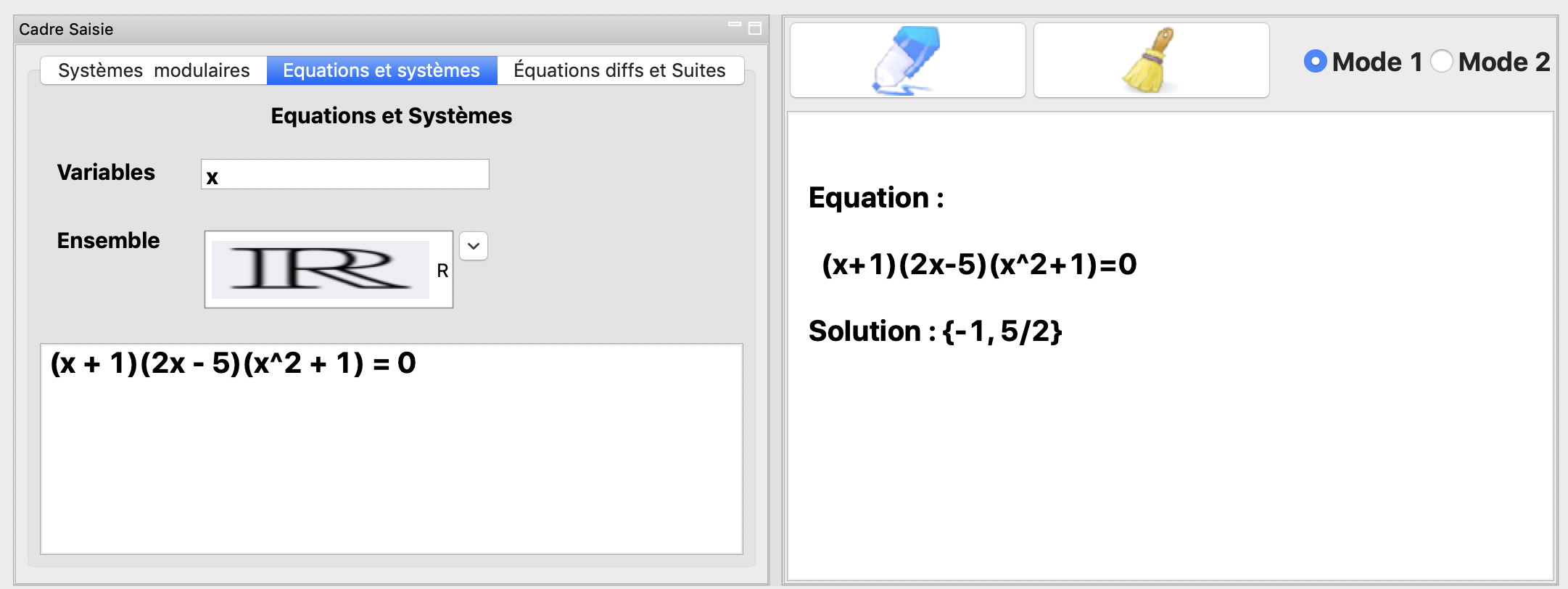
Vous pouvez aussi résoudre des équations dans un ensemble donné.
La résolution de l” équation \((x+1)(2x-5)(x^2+1)=0\) dans \(\mathbb{R}\)
Résolution avec des paramètres
Note
S’il y a des variables dans l’équation qui ne sont pas définies dans la zone des variables, alors on les considère comme des paramètres.
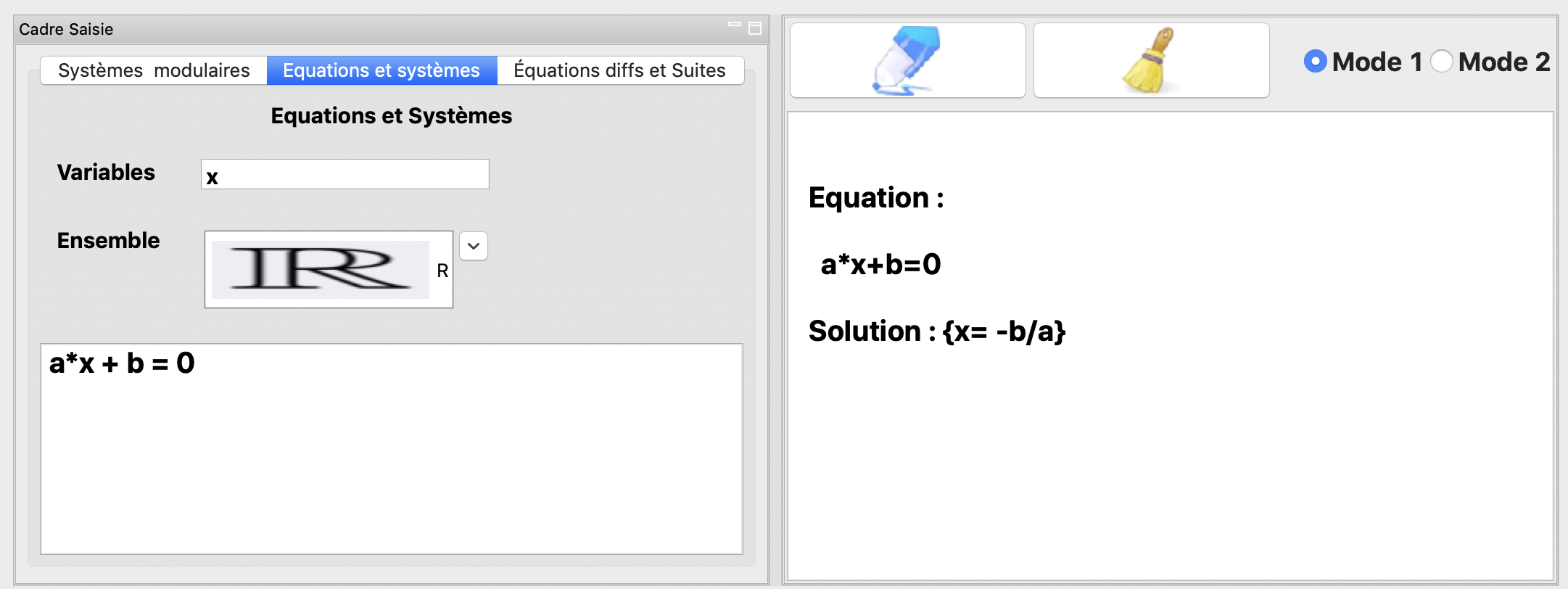
La résolution de l’inéquation \(x^2-3x+2<0\) dans \(\mathbb{R}\)
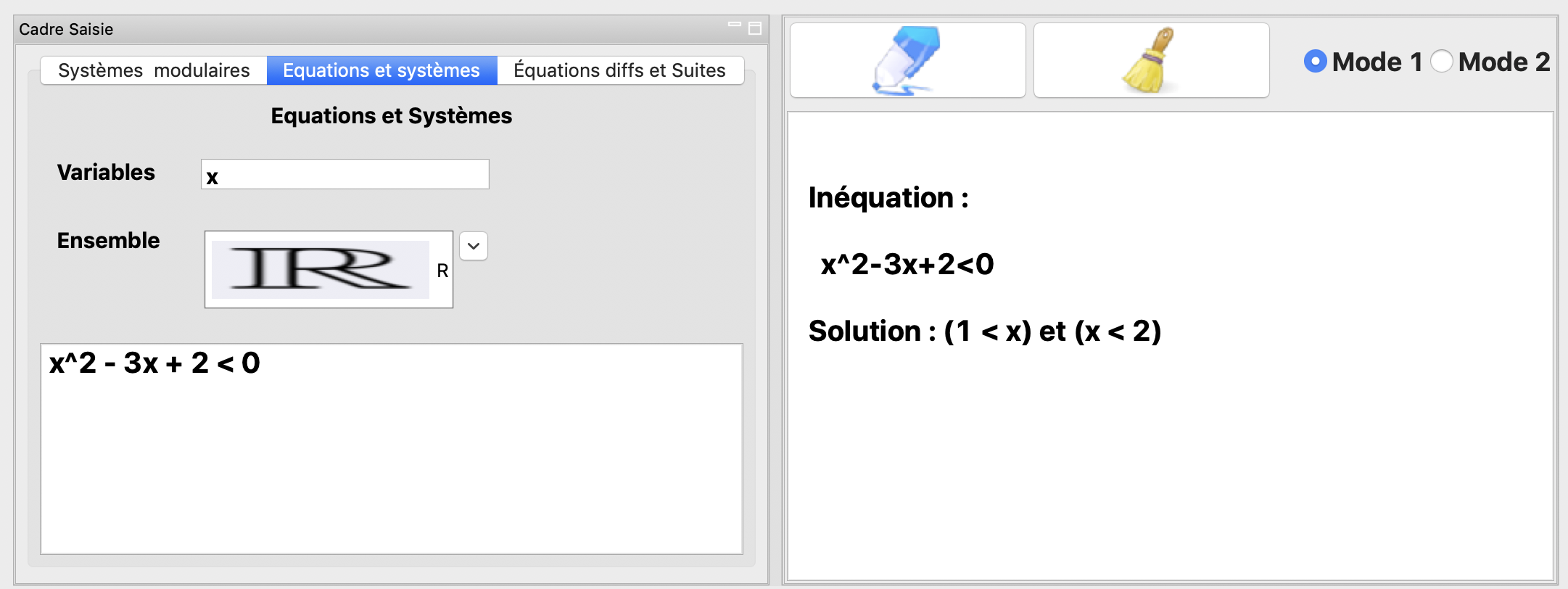
La résolution de l’inéquation \(x^2-3x+2\geq 0\) dans \(\mathbb{R}\)
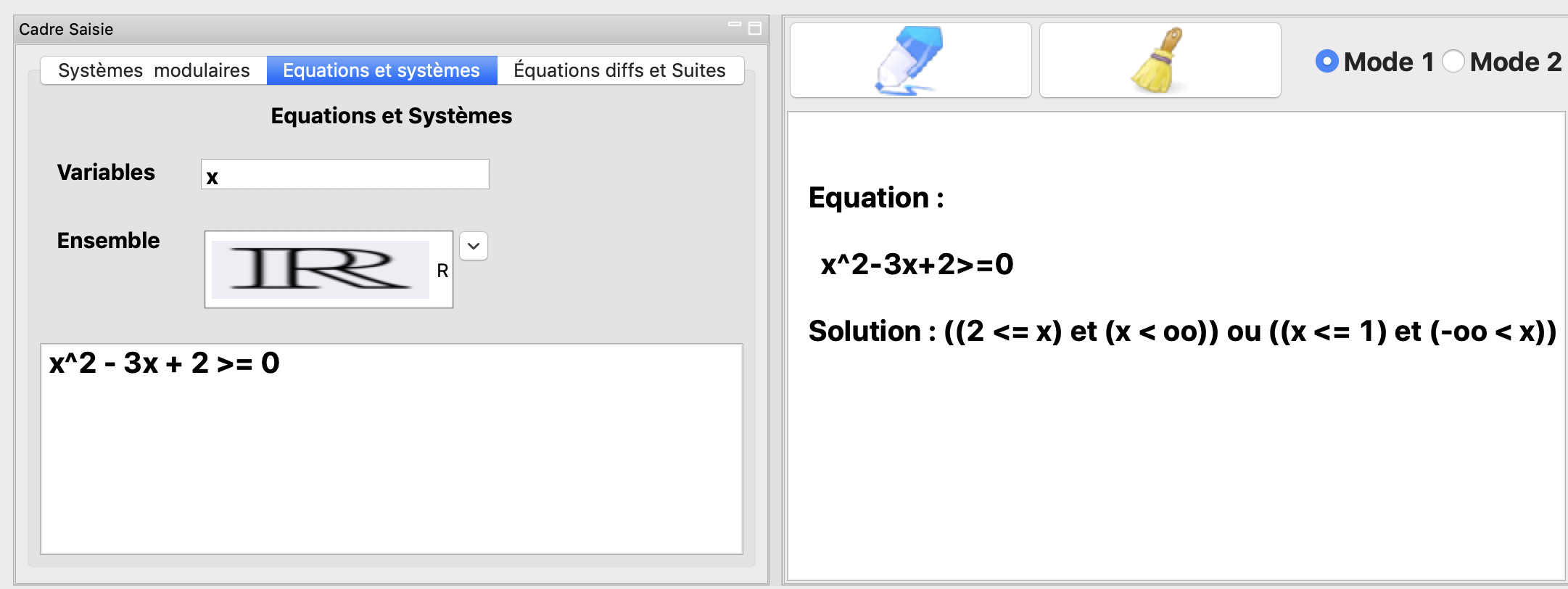
La résolution dans \(\mathbb{R}\) de \((x-1)(x+4)=0\text{ et } x>0\).
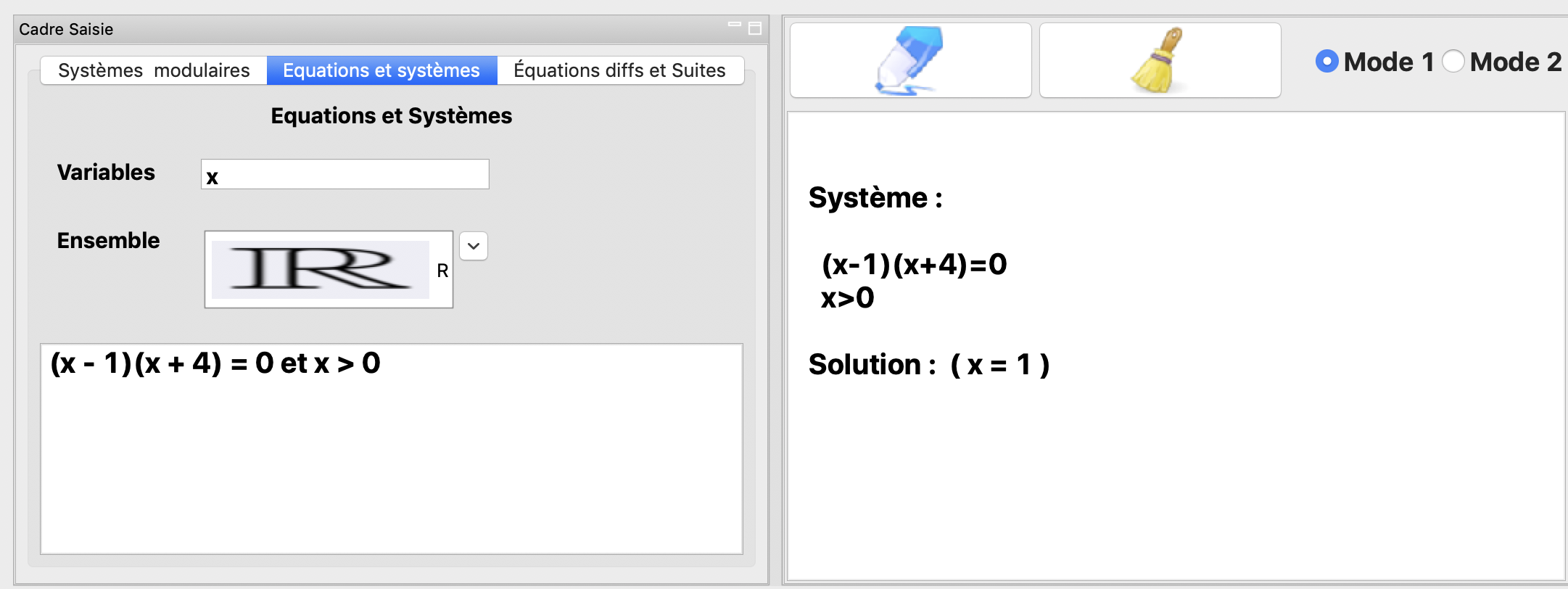
Systèmes linéaires et non linéaires¶
Pour saisir un système (ou une inéquation),
Saisir d’abord la première équation (ou inéquation) puis appuyer sur la touche ENTREE;
Puis Saisir la deuxième équation (ou inéquation) puis appuyer sur la touche ENTREE;
Et ainsi de suite jusqu’à la dernière équation (ou inéquation).
La résolution dans \(\mathbb{R}^2\) du système:
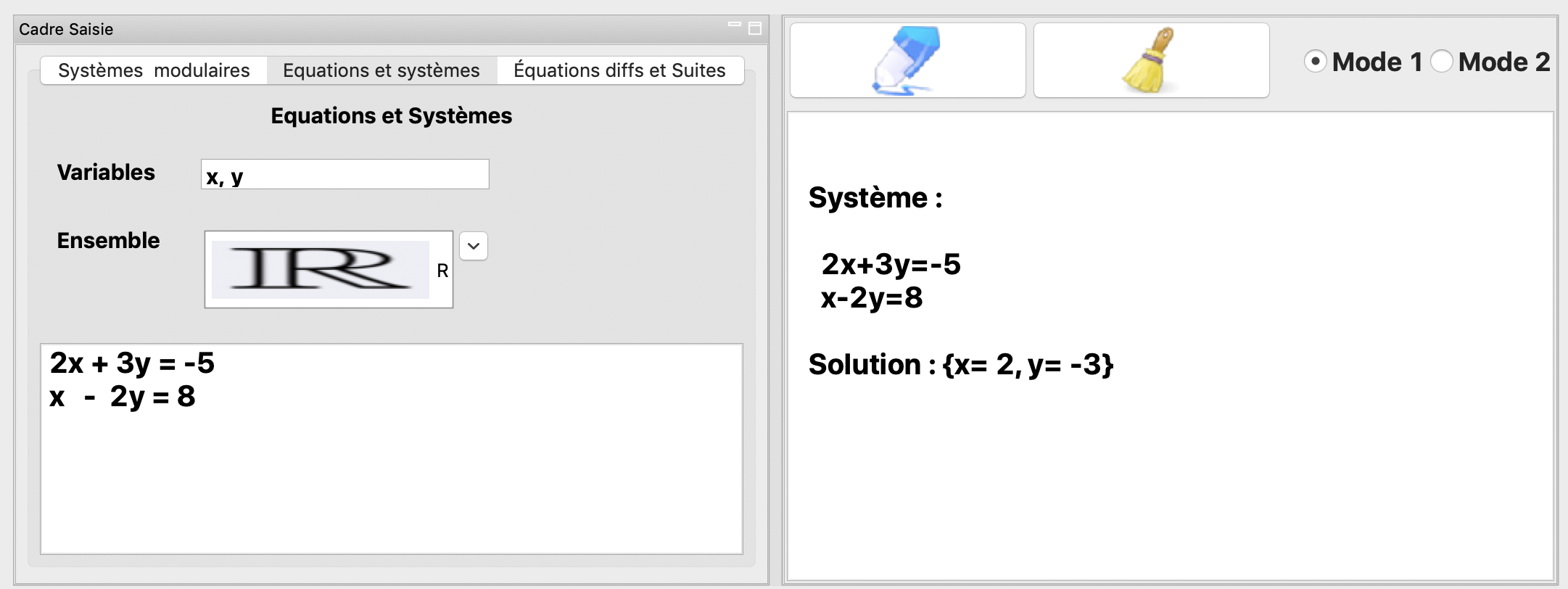
La résolution dans \(\mathbb{R}^3\) du système:
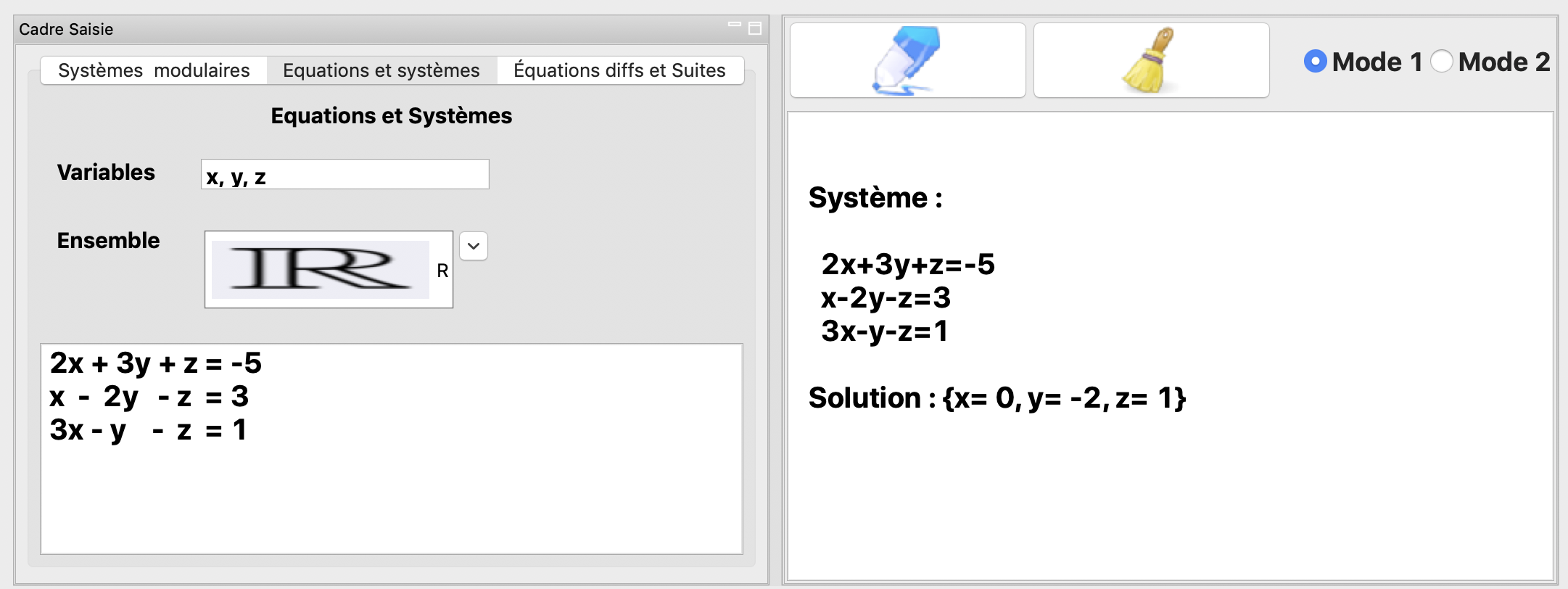
La résolution dans \(\mathbb{R}^3\) du système:
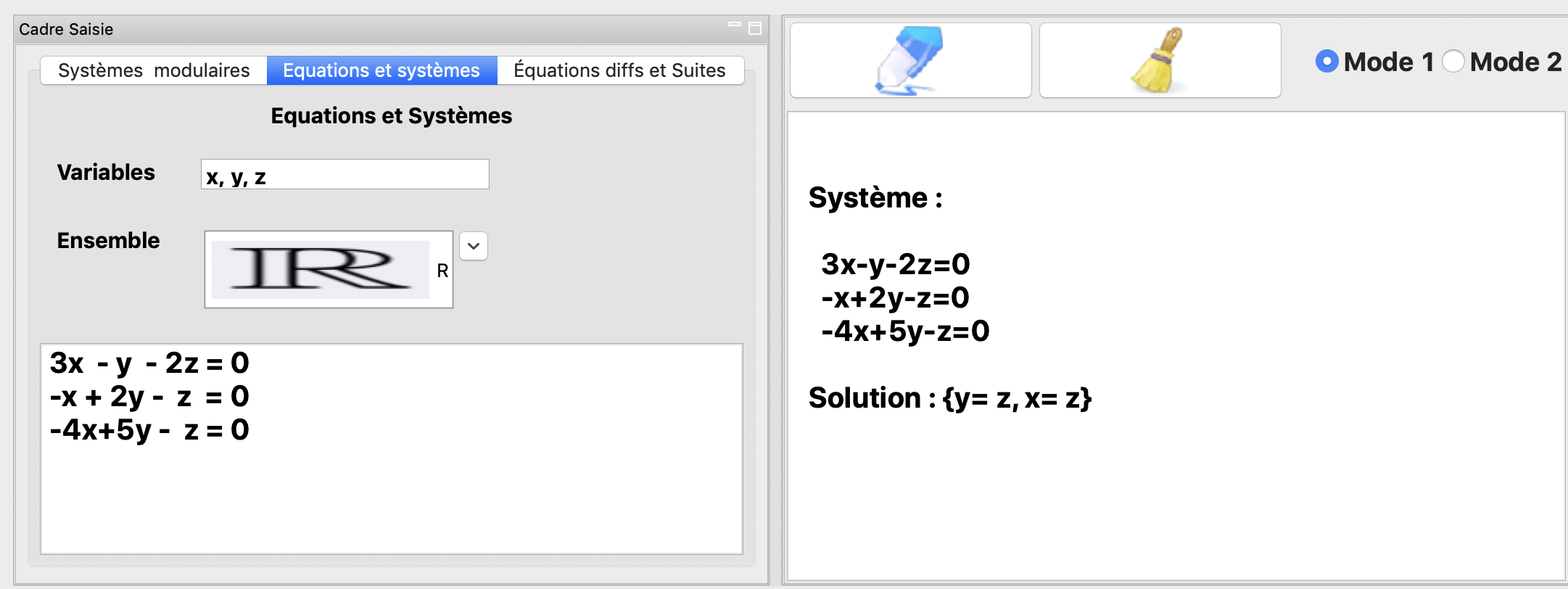
Équations différentielles¶
La résolution de l’équation différentielle \(y'''-3y''+3y'-y=0\)
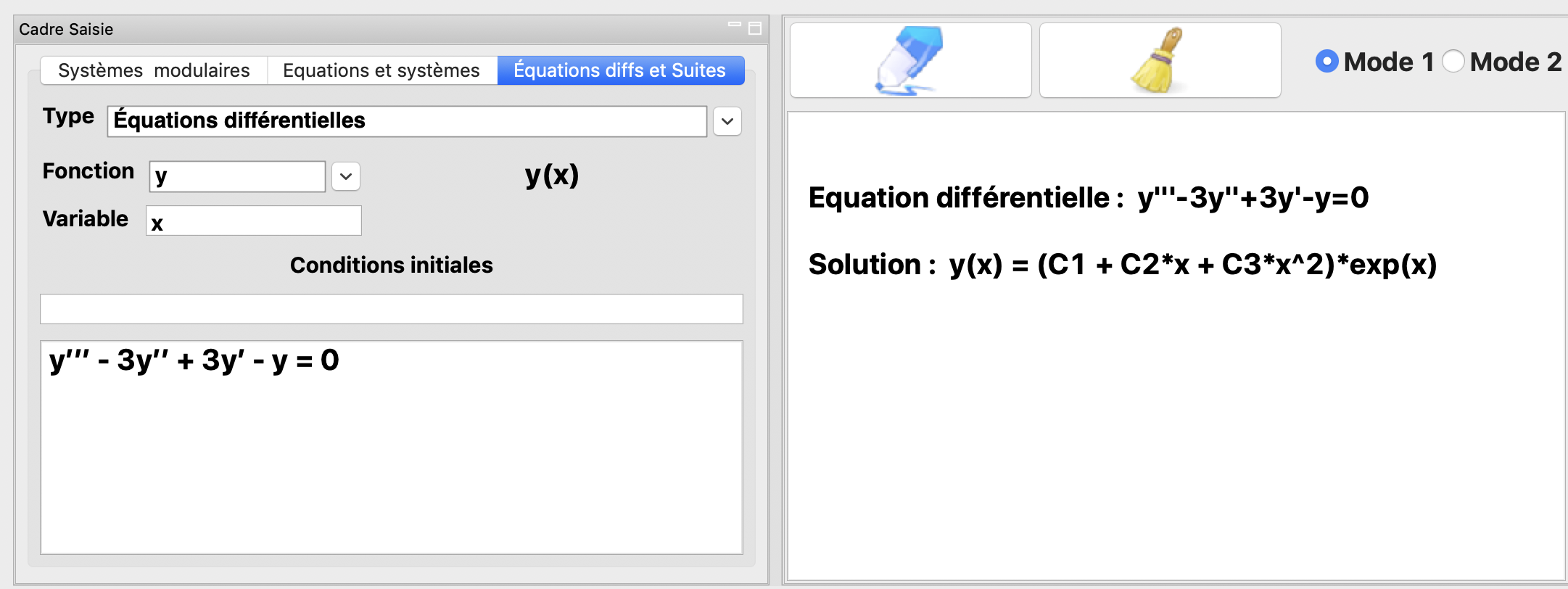
La résolution de l’équation différentielle \(y'''-3y''+3y'-y=0\) avec les conditions initiales \(y(0) = 0; y'(0)=1\) et \(y''(0)=1\).
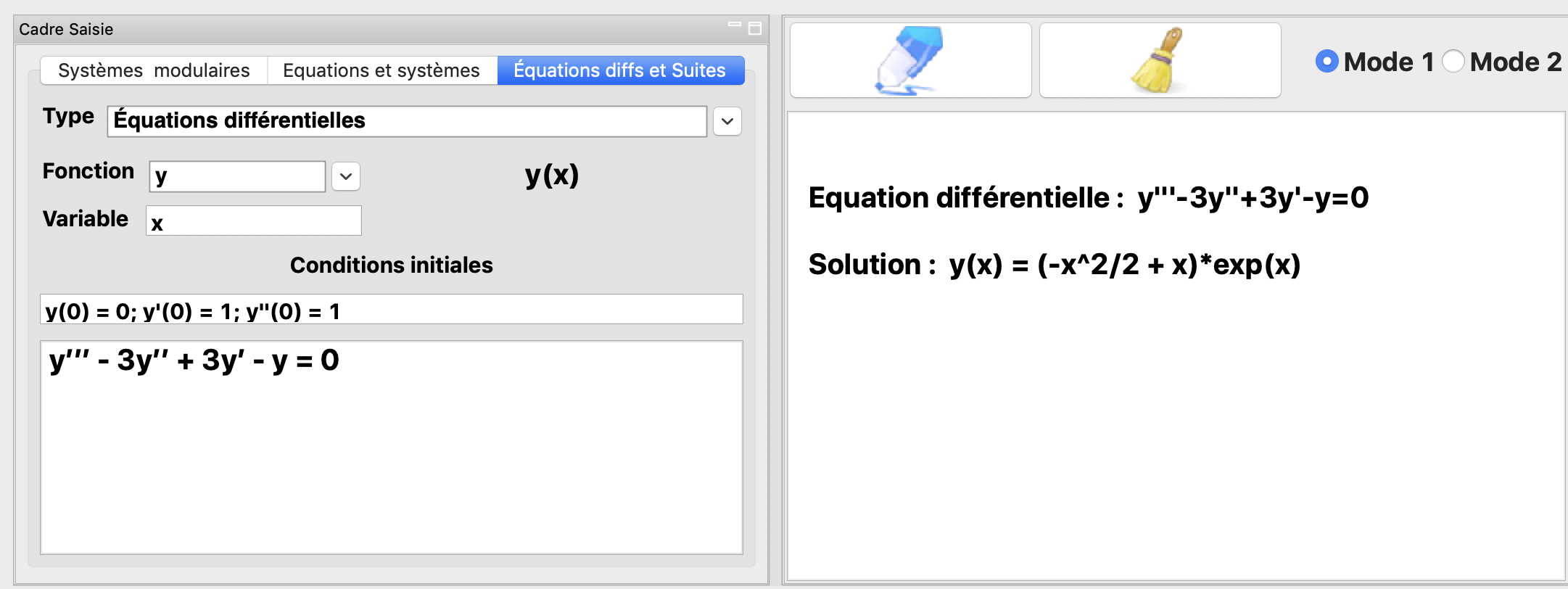
La résolution de l’équation différentielle \(y''+2y'+y=0\)
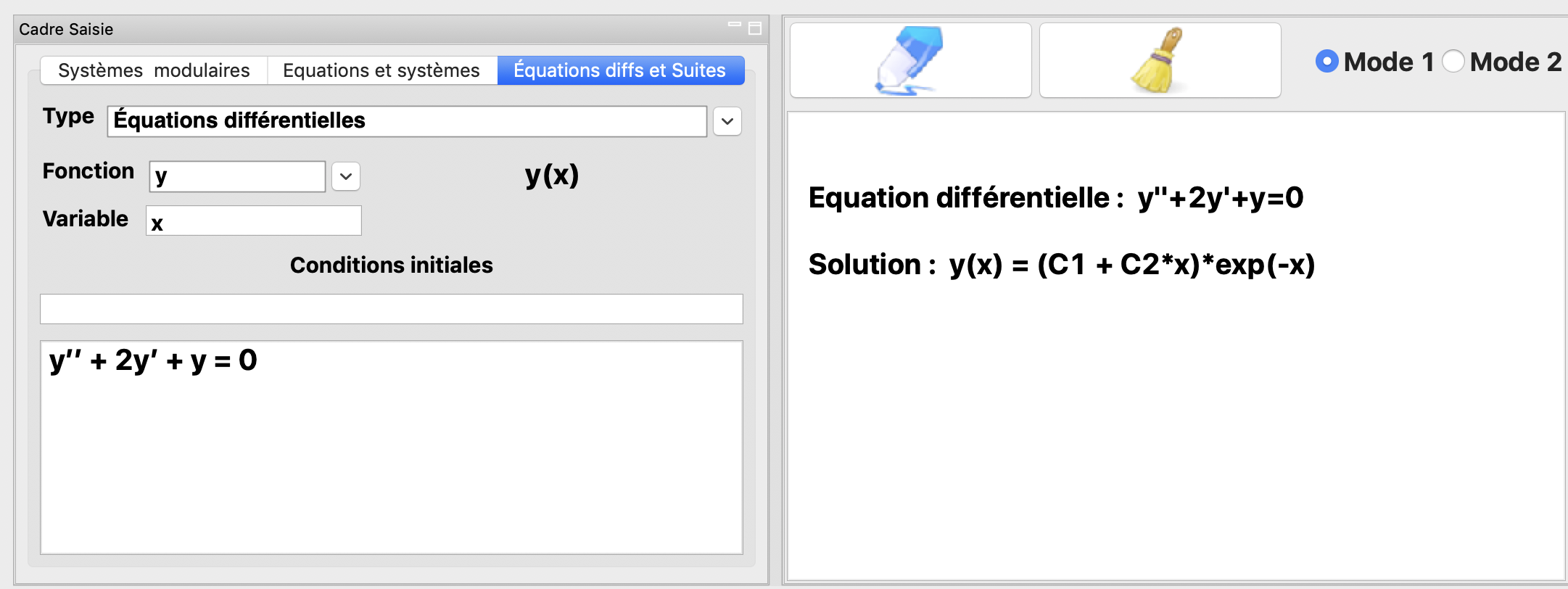
La résolution de l’équation différentielle \(y''+2y'+y=0\) avec les conditions initiales \(y(0)=1\) et \(y'(0)=2\).
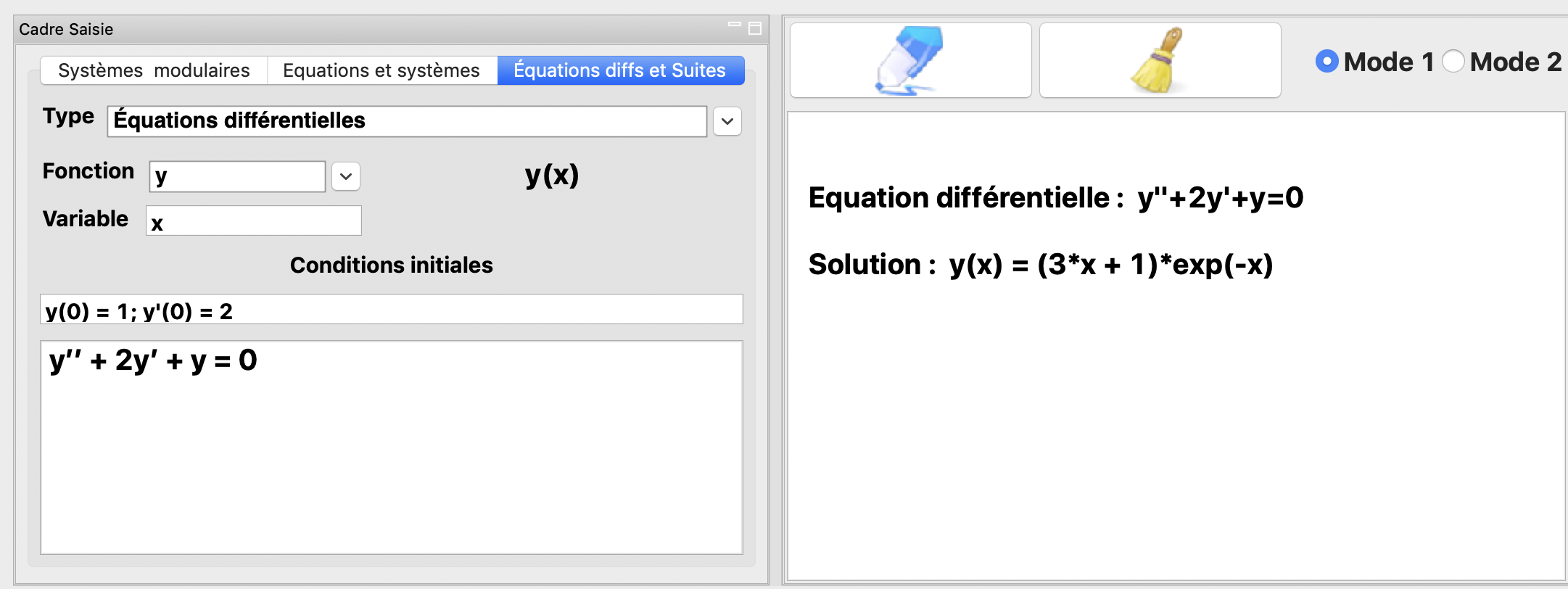
La résolution de l’équation différentielle \(y''+y=\cos(x)\)
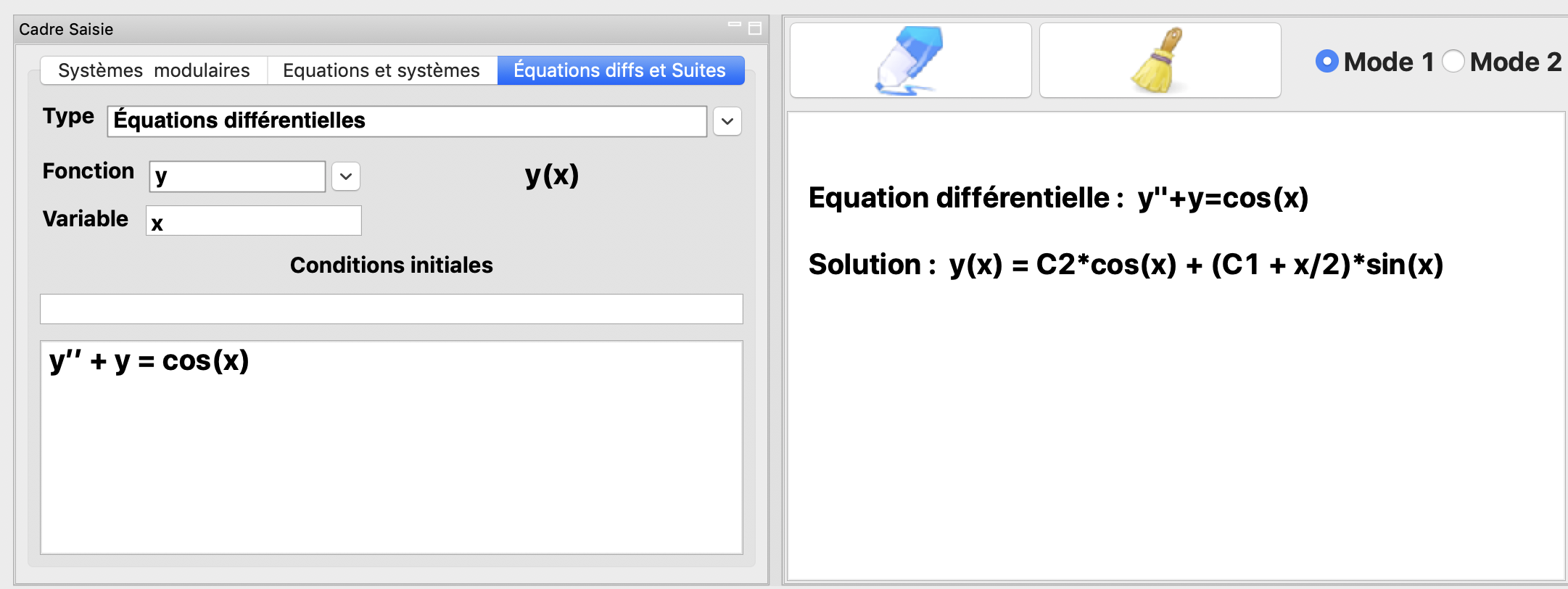
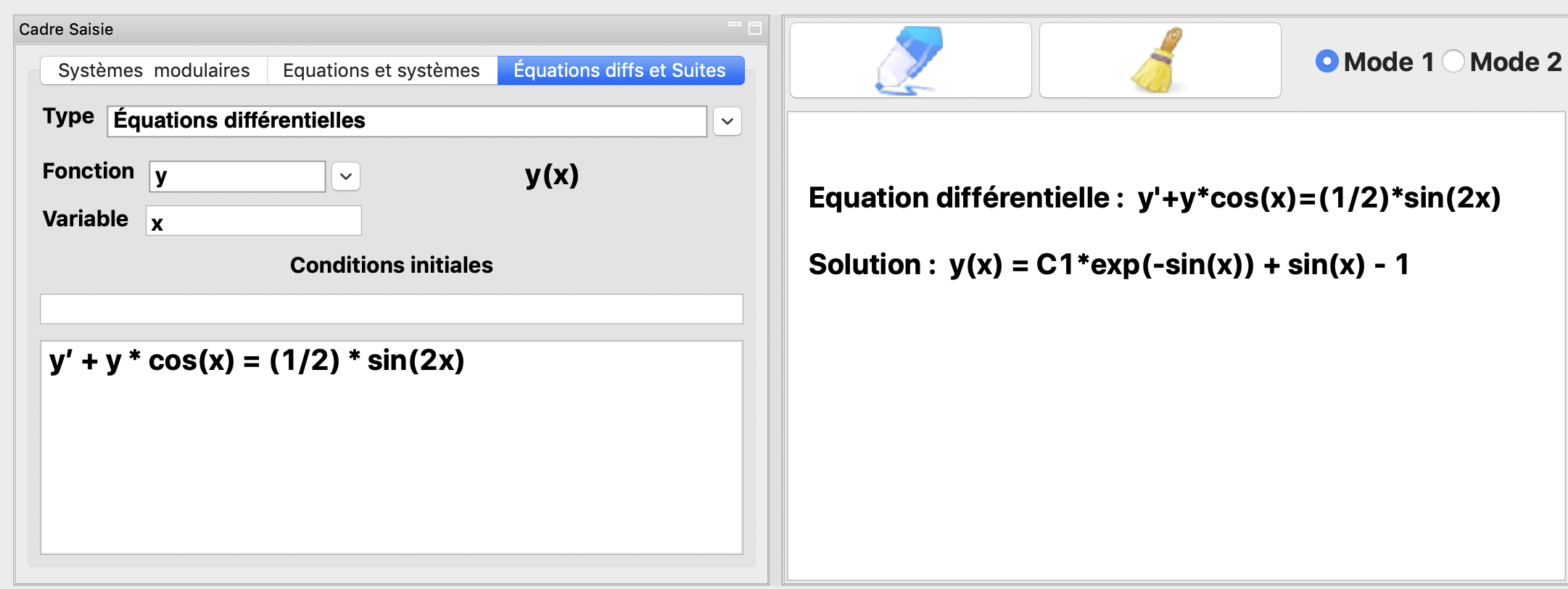
La résolution de l’équation différentielle \(y'+y\cos(x) = \frac{1}{2}\sin(2x)\)
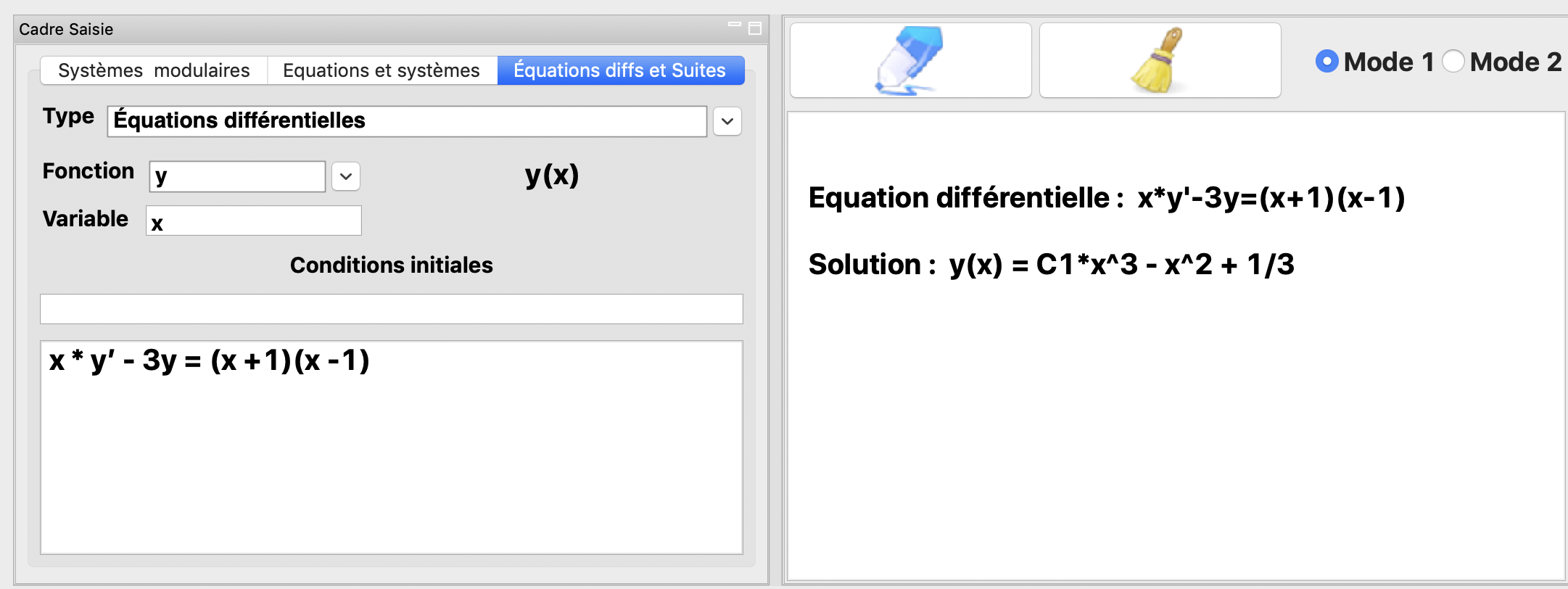
La résolution de l’équation différentielle \(xy'-3y=(x+1)(x-3)\)
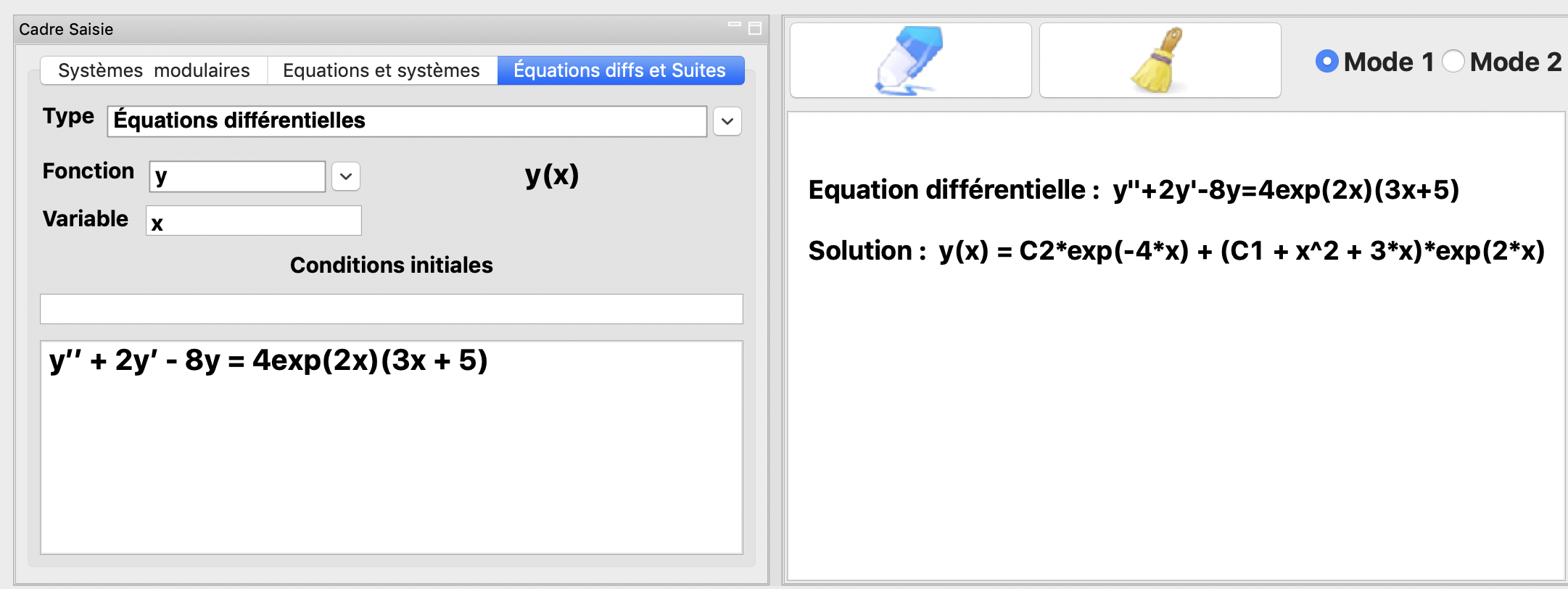
La résolution de l’équation différentielle \(y''+2y'-8y=4exp(2x)(3x+5)\)
Systèmes différentiels¶
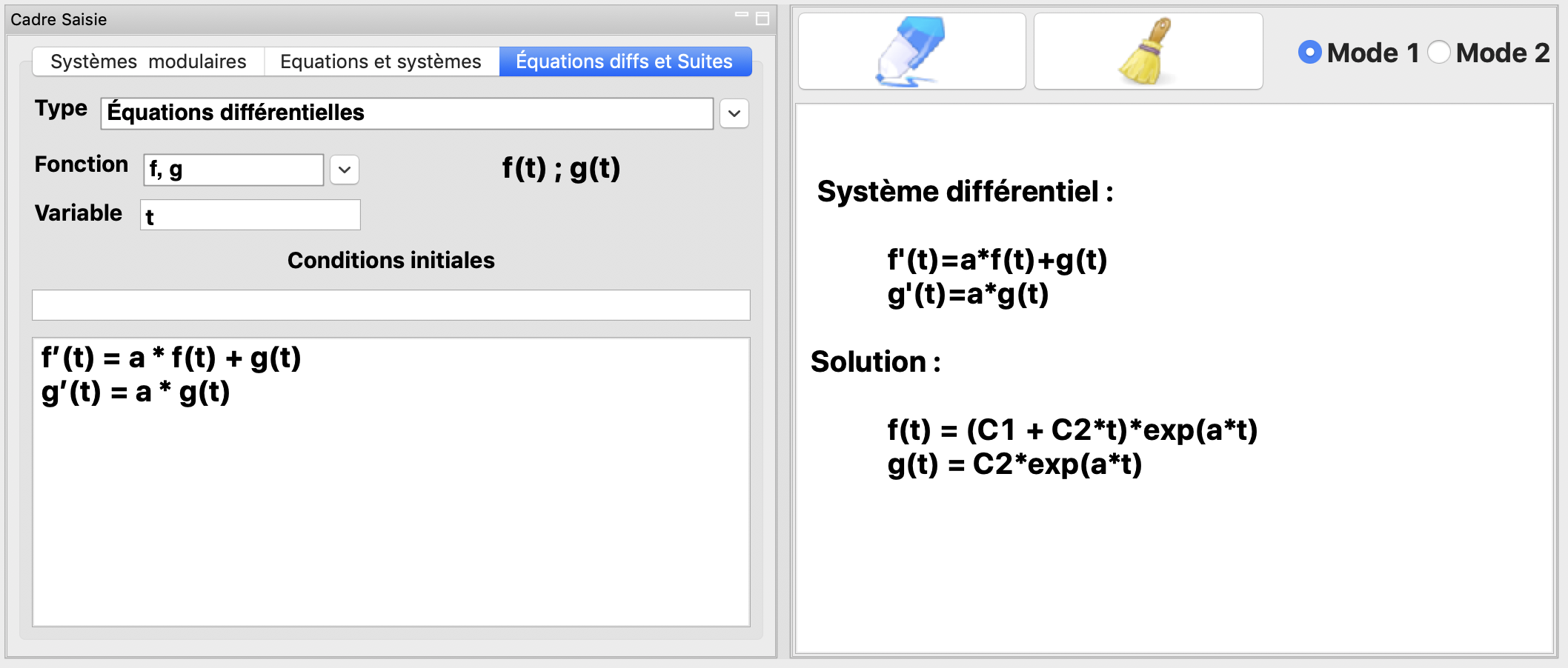
La résolution du système différentiel
avec \(a\in \mathbb{R}\).
La résolution du système différentiel
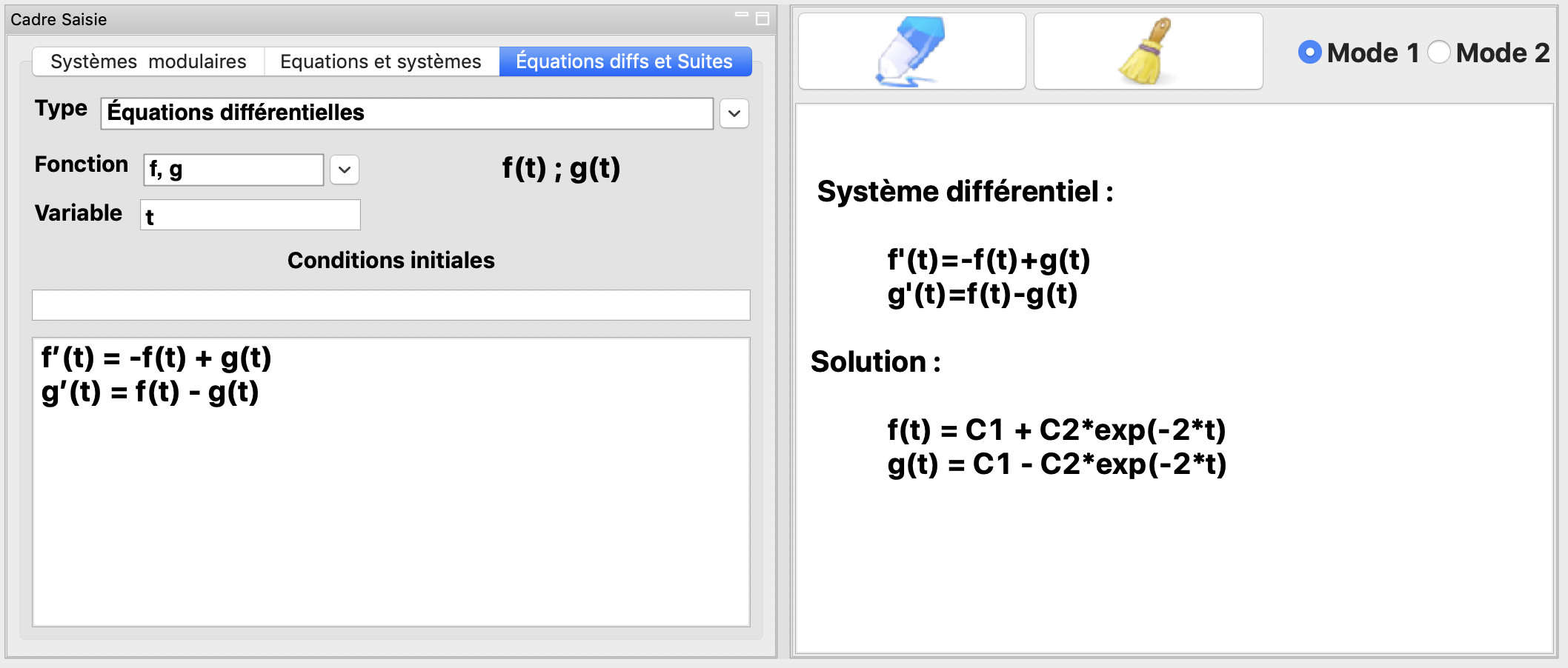
La résolution du système différentiel
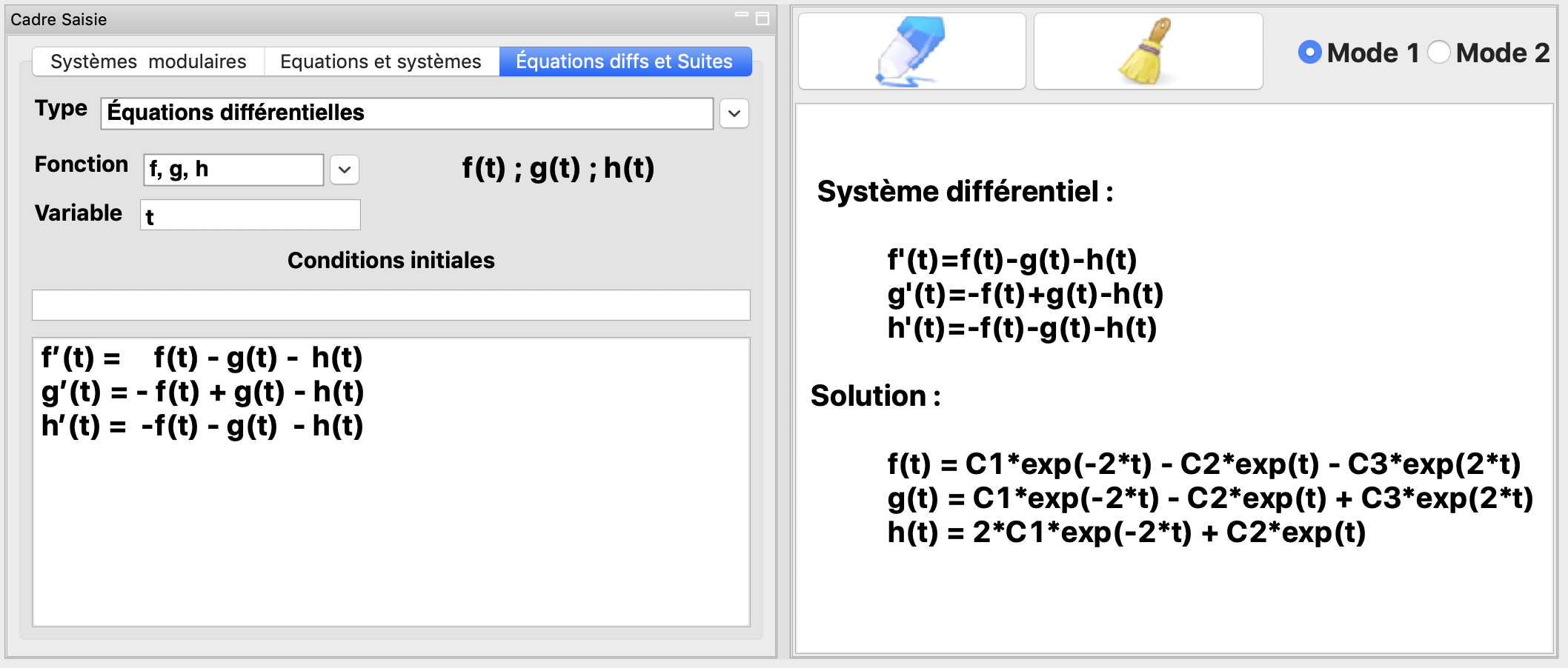
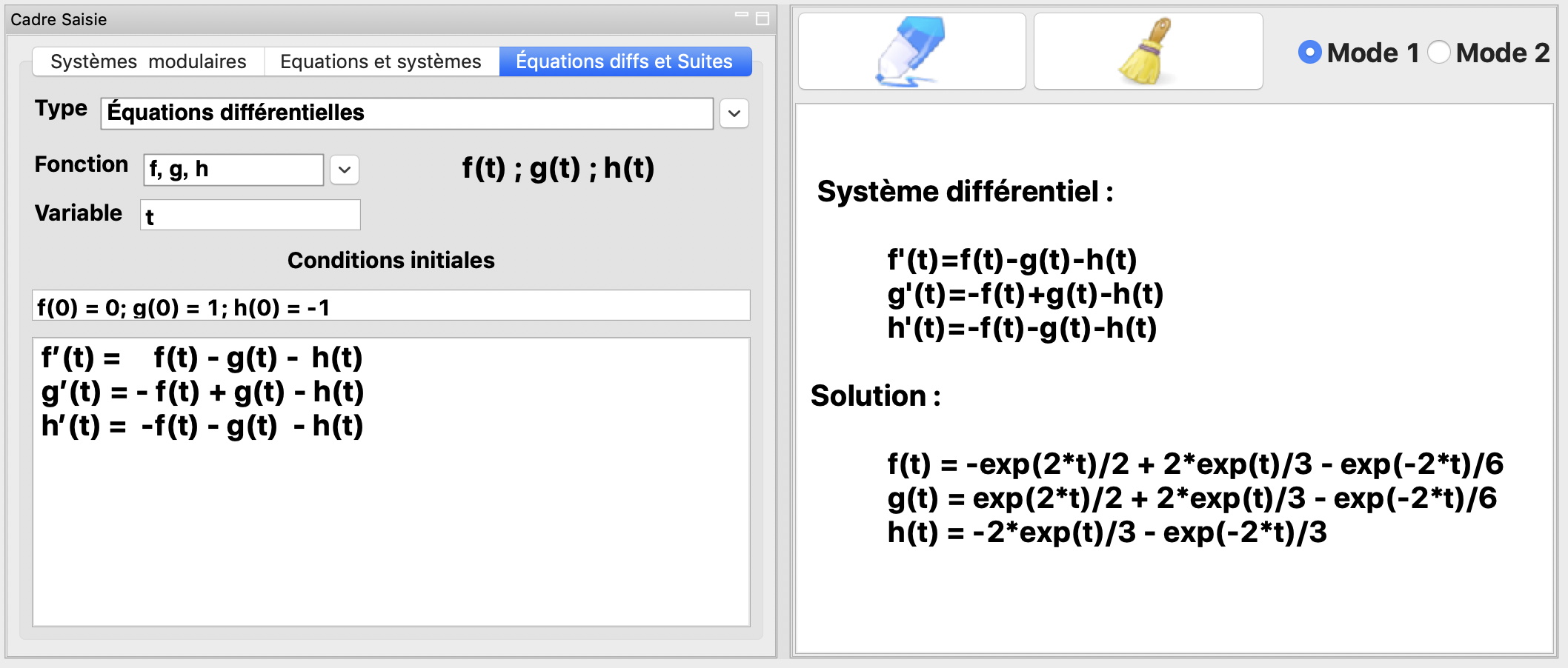
La résolution du système différentiel :
avec les conditions initiales \(f(0)=0; g(0)=1\) et \(h(0)=-1\).
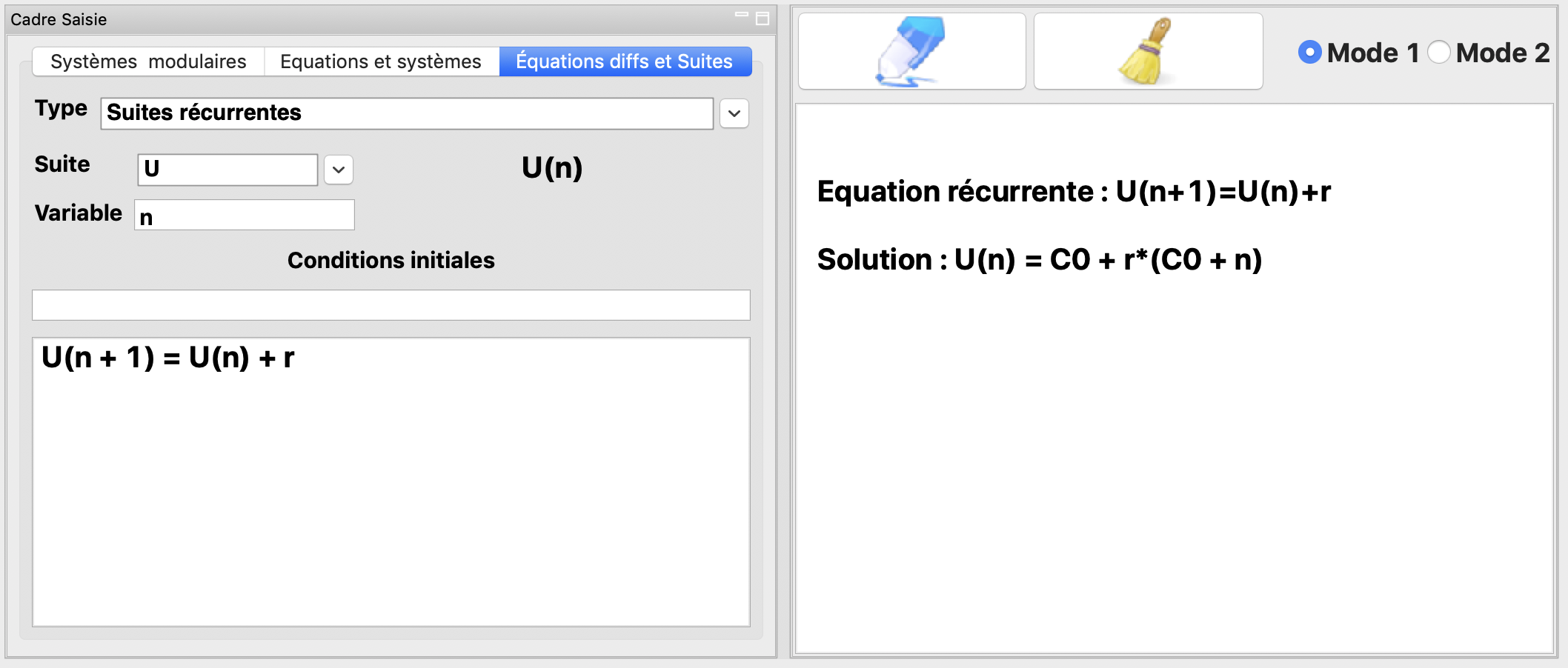
Suite récurrentes¶
La résolution de l’équation récurrente \(U(n+1)=U(n)+r\) avec \(r\in \mathbb{R}\).
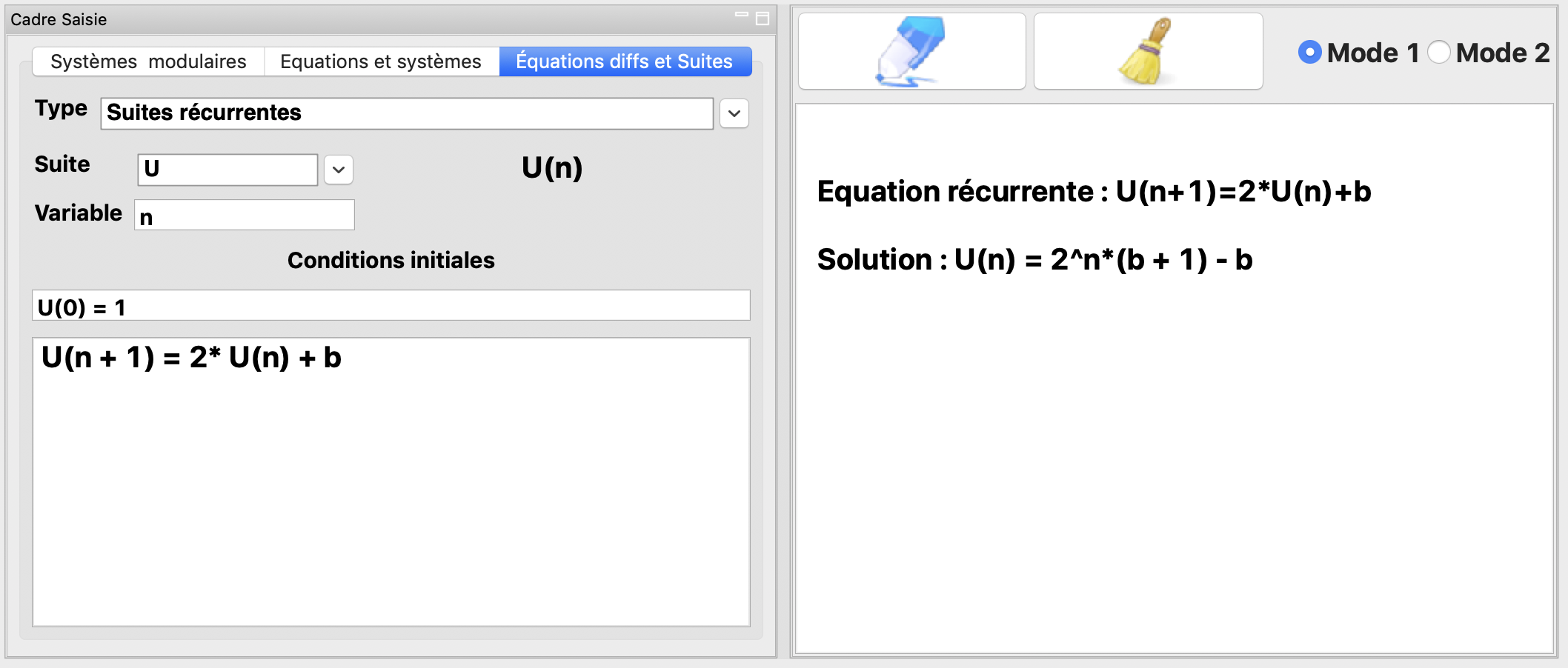
La résolution de l’équation récurrente \(U(n+1)=2U(n)+b\) avec \(b\in \mathbb{R}\) avec \(U(0)=1\).
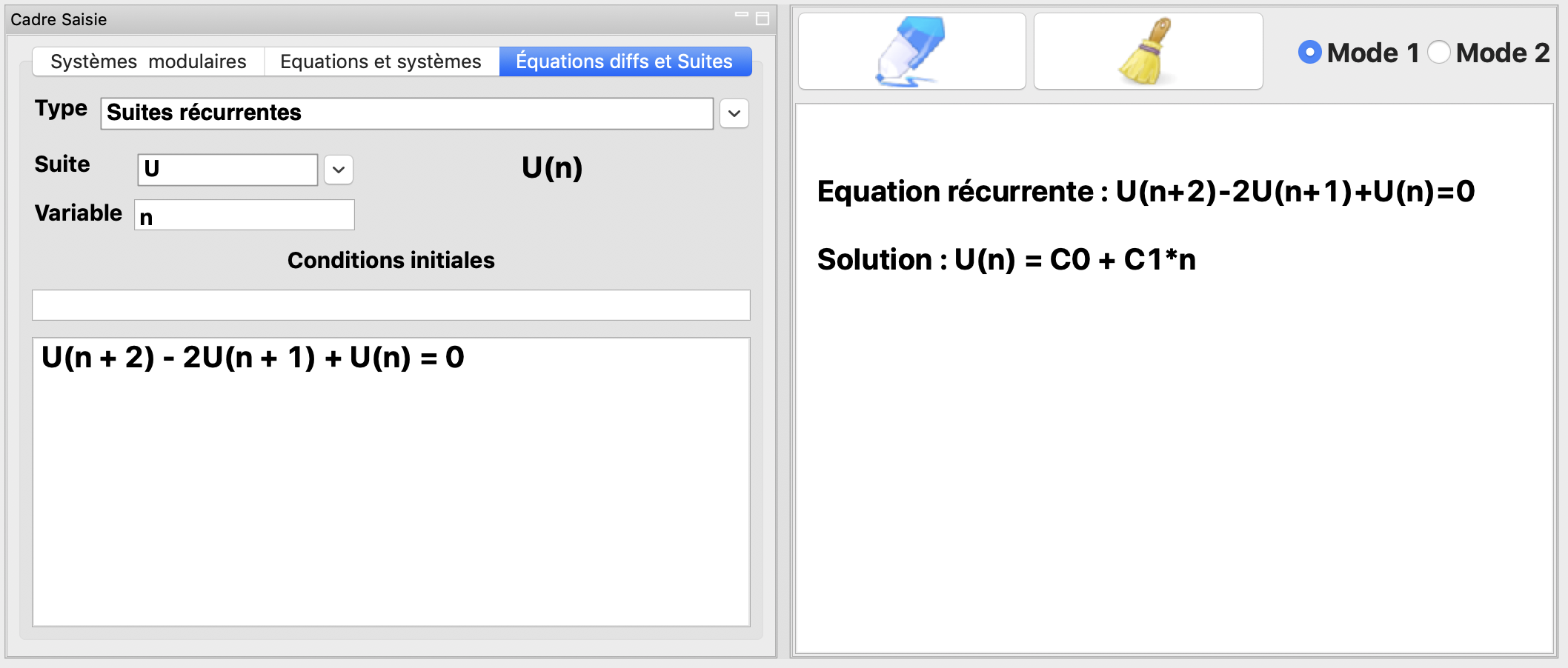
La résolution de l’équation récurrente \(U(n+2) -2U(n+1)+U(n)=0\).
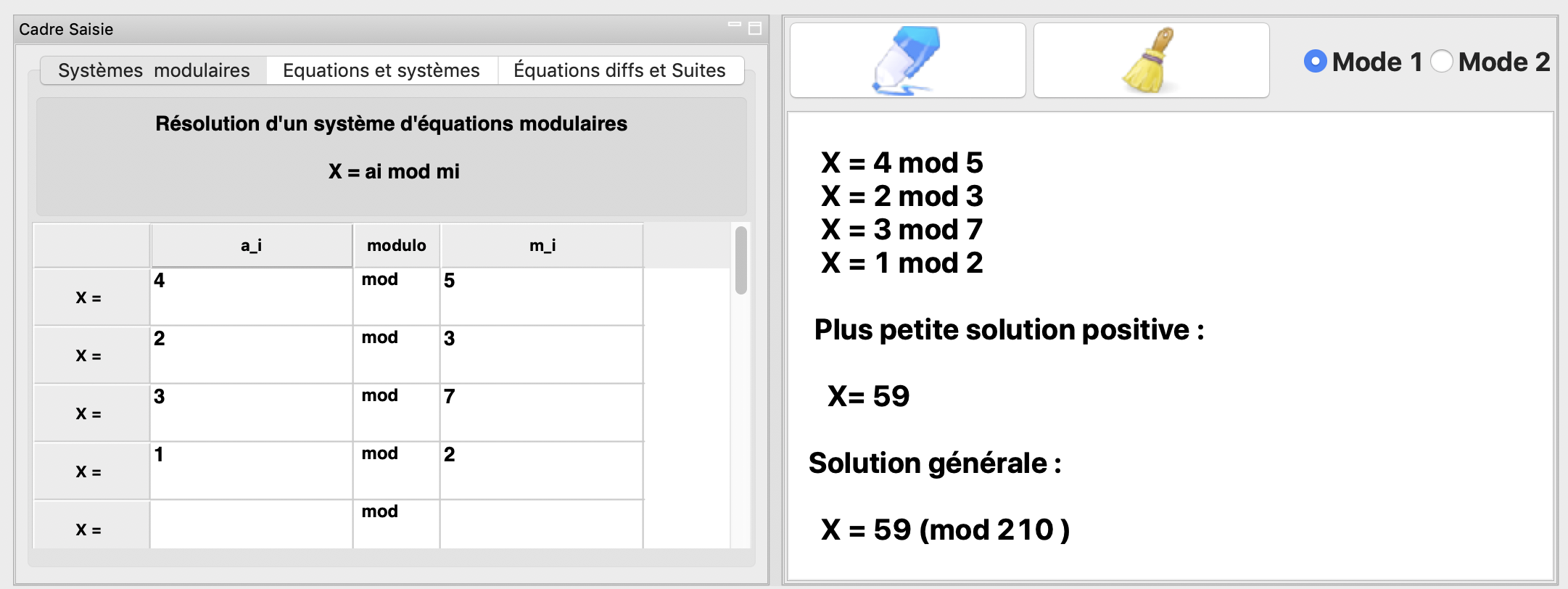
Systèmes modulaires¶
La résolution de quelques systèmes modulaires peut être faite en utilisant le théorème du reste Chinois.
Exemple : la résolution du système modulaire