Statistique descriptive univariée¶
Pour la statistique descriptive à une seule variable, on peut déterminer les caractéristiques suivantes.
la moyenne
la moyenne empirique
la moyenne quadratique
la moyenne géométrique
la moyenne harmonique
la variance
la variance empirique
le moment d’ordre alpha
l’écart type
l’écart type empirique
le mode (et la la classe modale dans le cas d’un caractère continu)
la médiane (et la la classe médiane dans le cas d’un caractère continu)
les quartiles Q1 et Q3
l’écart moyen absolu
l’écart médian absolu
l’écart inter-quartiles
le coefficient de variation
le coefficient de dissymétrie
le coefficient d’asymétrie de Fisher
le coefficient d’asymétrie de Yule
le coefficient d’asymétrie de Pearson
le coefficient d’aplatissement de Pearson
le coefficient d’aplatissement de Fisher
La saisie de données est très simple comme l’ullistrent les exemples ci_dessous.
Caractères discrets¶
Exemple 1: Série statistique
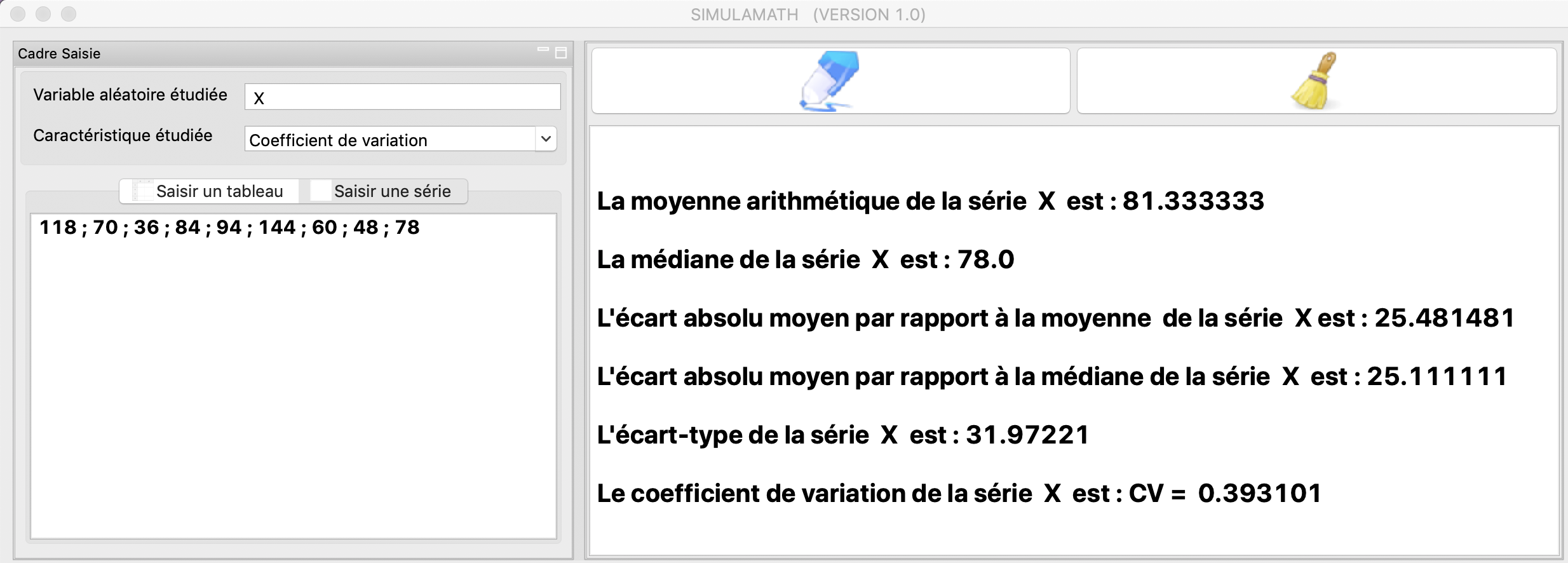
La série ci-après représente la superficie (en \(m^2\)) des neuf appartements d’une résidence : 118 ; 70 ; 36 ; 84 ; 94 ; 144 ; 60 ; 48 ; 78
Déterminer la moyenne arithmétique et la médiane de cette distribution.
Calculer les caractéristiques de dispersion suivantes : écart absolus moyen par rapport à la moyenne et à la médiane, l’écart type et le coefficient de variation.
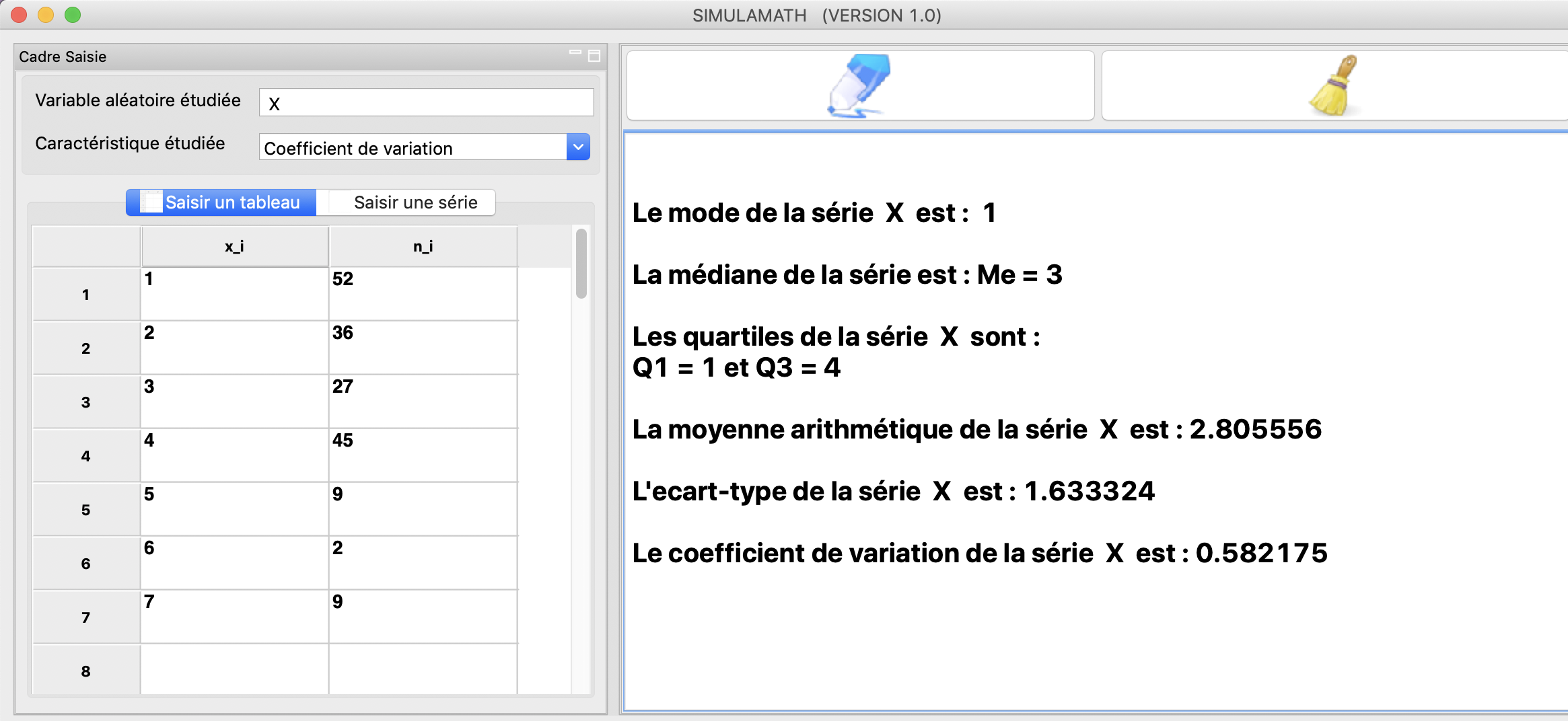
Exemple 2: Série statistique sous forme de tableau.
Dans une librairie, 180 auteurs ont été répartis suivant le nombre de manuels qu’ils ont écrits.
\(x_i\) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|---|---|---|---|---|---|---|---|
\(n_i\) |
52 |
36 |
27 |
45 |
9 |
2 |
9 |
Déterminer le mode, la médiane et les quartiles \(Q_1\) et \(Q_3\).
Calculer la moyenne arithmétique, l’écart type et le coefficient de variation de cette série.
Caractères Continus¶
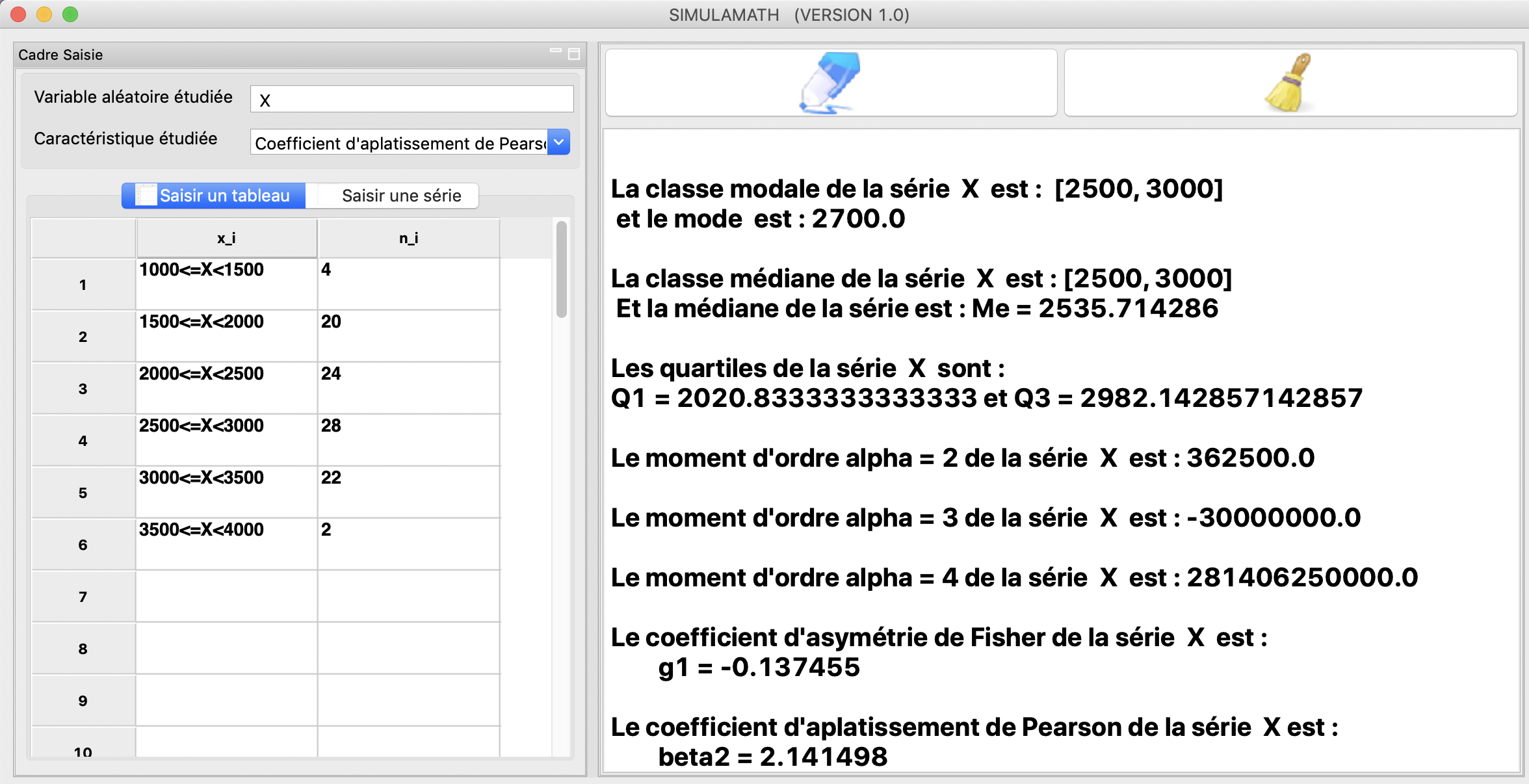
Exemple 3: Données groupées en classes d’amplitudes égales
Le tableau ci-dessous donne la distribution du nombre de commandes en fonction du montant des commandes \(X\), pour les six derniers mois du GIE LIGGEEY.
\(X\) |
\(1000 \leq X<1500\) |
\(1500 \leq X<2000\) |
\(2000 \leq X<2500\) |
\(2500 \leq X<3000\) |
\(3000 \leq X<3500\) |
\(3500 \leq X<4000\) |
|---|---|---|---|---|---|---|
Effectifs |
\(\ \ \ \ \ \ \ \ \ 4\ \ \ \ \ \ \ \ \) |
\(\ \ \ \ \ \ \ \ \ 20\ \ \ \ \ \ \ \ \) |
\(\ \ \ \ \ \ \ \ \ 24\ \ \ \ \ \ \ \ \) |
\(\ \ \ \ \ \ \ \ \ 28\ \ \ \ \ \ \ \ \) |
\(\ \ \ \ \ \ \ \ \ 22\ \ \ \ \ \ \ \ \) |
\(\ \ \ \ \ \ \ \ \ 2\ \ \ \ \ \ \ \ \) |
Déterminer la classe modale, le mode, la médiane et les quartiles \(Q_1\) et \(Q_3\).
Calculer les moments centrés d’ordre \(2, 3\) et \(4\) de cette distribution.
Calculer le coefficient d’asymétrie de Fisher et le coefficient d’aplatissement de Pearson.
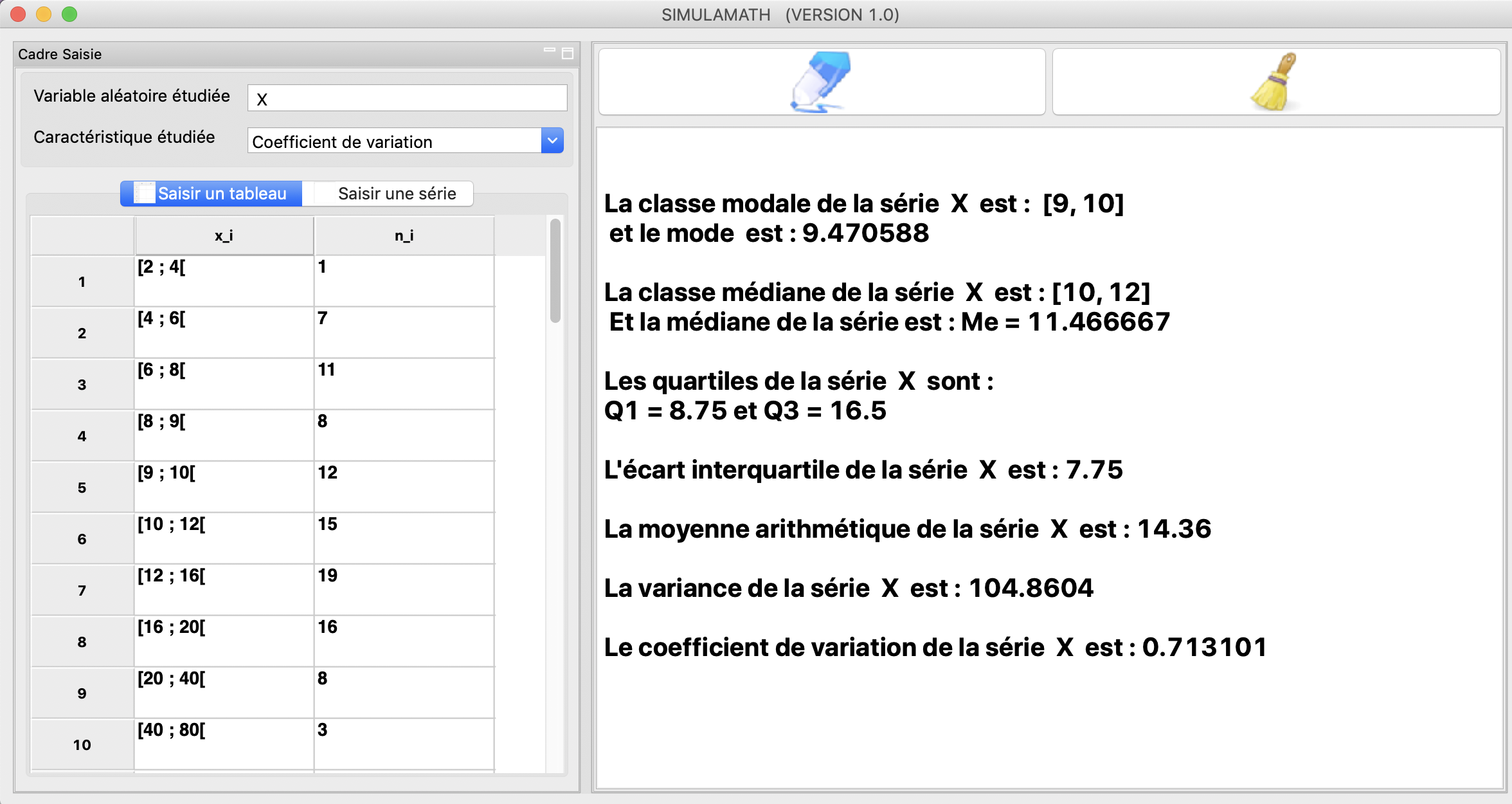
Exemple 4: Données groupées en classes d’amplitudes inégales
Le tableau ci-après fournit la répartition en pourcentage des habitants d’une commune, selon le montant annuel de leurs impôts locaux (en milliers de francs).
Classes |
[2 ; 4[ |
[4 ; 6[ |
[8 ; 9[ |
[9 ; 10[ |
[10 ; 12[ |
[12 ; 16[ |
[16 ; 20[ |
[20 ; 40[ |
[40 ; 60[ |
[60 ; 80[ |
|---|---|---|---|---|---|---|---|---|---|---|
Effectifs |
1 |
7 |
11 |
8 |
12 |
15 |
19 |
16 |
8 |
3 |
Déterminer la classe modale, le mode, la médiane et les quartiles \(Q_1\) et \(Q_3\).
Calculer la moyenne arithmétique de cette série, l’écart interquartile, la variance et le coefficient de variation.