Solving Equations, Inequations and Systems.

Equations and Inequations

To solve an equation (or an inequation) with SimulaMath:

  • Enter the equation (or inequation) in the left panel,

  • Specify the variable(s) in the variables area,

  • Then click on the display button.

  • The solution to the equation \((x+1)(2x-5)(x^2+1)=0\) over \(\mathbb{R}\).

Note

You must specify the variables in the variables area

../_images/solving-eq1.en.PNG

Note

You can also solve equations in a given set.

  • Solving the equation \((x+1)(2x-5)(x^2+1)=0\) over \(\mathbb{C}\)

../_images/solving-eq2.en.PNG

  • Resolution with parameters

Note

If there are variables in the equation that are not defined in the variables area, then they are considered as parameters.

Let us solve the equation \(ax+b = 0\) when \(x\in \mathbb{R}\).

../_images/solving-eq3.en.PNG

  • The solution of the inequation \(x^2-3x+2 \geq 0\) in \(\mathbb{R}\)

../_images/solving-ineq1.en.PNG

  • The resolution in \(\mathbb{R}\) of \((x-1)(x+4)=0\text{ and } x>0\).

../_images/solving-ineq2.en.PNG

Linear and non-linear systems

To enter a system (or an inequation),

  1. First enter the first equation (or inequation) and then press the ENTER key;

  2. Then enter the second equation (or inequation) and press ENTER;

  3. And so on until the last equation (or inequation).

  • The solution in \(\mathbb{R}^2\) of the system:

\[\begin{split}\begin{cases} 2x+3y&=-5\\ x-2y&=8 \end{cases}\end{split}\]
../_images/solving-sys1.en.PNG

  • The resolution in \(\mathbb{R}^3\) of the system:

\[\begin{split}\begin{cases} 2x+3y+z&=-5\\ x-2y-z&=3\\ 3x-y-z&=1 \end{cases}\end{split}\]
../_images/solving-sys2.en.PNG

  • The resolution in \(\mathbb{R}^3\) of the system:

\[\begin{split}\begin{cases} 3x-y-2z&=0\\ x+2y-z&=0\\ -4x+5y-z&=0 \end{cases}\end{split}\]
../_images/solving-sys3.en.PNG

Differential Equations

  • The resolution of the differential equation \(y'''-3y''+3y'-y=0\)

../_images/diff1.en.PNG

  • The resolution of the differential equation \(y'''-3y''+3y'-y=0\) with the initial conditions \(y(0) = 0; y'(0)=1\) and \(y''(0)=1\).

../_images/diff1-ics.en.PNG

  • The resolution of the differential equation \(y''+2y'+y=0\).

../_images/diff2.en.PNG

  • The solution of the differential equation \(y''+2y'+y=0\) with the initial conditions \(y(0)=1\) and \(y'(0)=2\).

../_images/diff2-ics.en.PNG

  • The solution of the differential equation \(y''+y=\cos(x)\)

../_images/diff3.en.PNG

  • The solution of the differential equation \(xy'-3y=(x+1)(x-3)\)

../_images/diff5.en.PNG

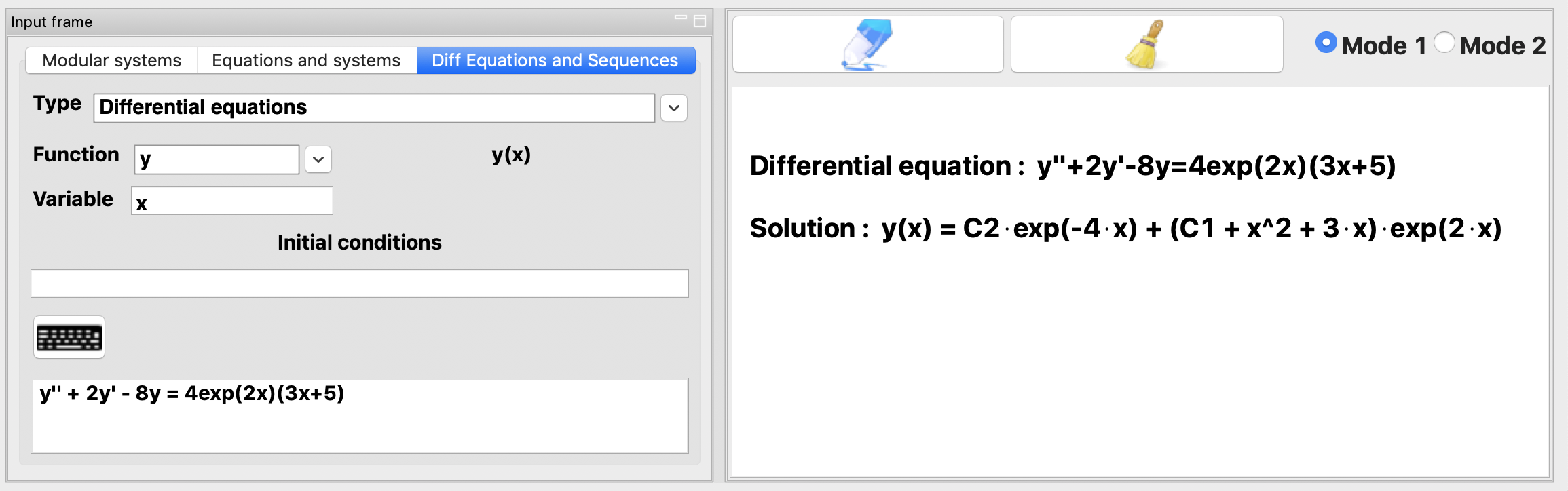
  • Solving the differential equation \(y''+2y'-8y=4exp(2x)(3x+5)\)

../_images/diff6.en.png

Differential Systems

  • The resolution of the differential system

\[\begin{split}\begin{cases} f'(t)&=af(t) + g(t)\\ g'(t)&=ag(t) \end{cases}\end{split}\]

with \(a\in \mathbb{R}\).

../_images/2diff1.en.PNG

  • The resolution of the differential system

\[\begin{split}\begin{cases} f'(t)&=-f(t) + g(t)\\ g'(t)&= f(t) - g(t) \end{cases}\end{split}\]
../_images/2diff2.en.PNG

  • The resolution of the differential system

\[\begin{split}\begin{cases} f'(t)&=f(t) - g(t) -h(t)\\ g'(t)&=-f(t)+g(t)-h(t)\\ h'(t)&=-f(t)-g(t)+h(t) \end{cases}\end{split}\]
../_images/3diff1.en.PNG

  • The resolution of the differential system :

\[\begin{split}\begin{cases} f'(t)&=f(t) - g(t) -h(t)\\ g'(t)&=-f(t)+g(t)-h(t)\\ h'(t)&=-f(t)-g(t)+h(t) \end{cases}\end{split}\]

with initial conditions \(f(0)=0; g(0)=1\) and \(h(0)=-1\).

../_images/3diff2.en.PNG

Recurrent Sequences

  • The solution of the recurrent equation \(U(n+1)=U(n)+r\) with \(r\in \mathbb{R}\).

../_images/sequence1.en.PNG

  • The solution of the recurrent equation \(U(n+1)=2U(n)+b\) with \(b\in \mathbb{R}\) with \(U(0)=1\).

../_images/sequence2.en.PNG

  • The solution of the recurrent equation \(U(n+2) -2U(n+1)+U(n)=0\).

../_images/sequence3.en.PNG

Modular Systems

The solution of some modular systems can be done by using the Chinese remainder theorem.

  • Example: solving the modular system

\[\begin{split}\begin{cases} x&\equiv 4 \ \mathrm{mod}\ \ 5\\ x&\equiv 2 \ \mathrm{mod}\ 3\\ x&\equiv 3 \ \mathrm{mod}\ 7\\ x&\equiv 1 \ \mathrm{mod}\ 2 \end{cases}\end{split}\]
../_images/modular.en.PNG